Es ist bekanntlich leicht, die Nullstellen einer Parabelfunktion zu visualisieren, wenn diese reell sind: Graph zeichnen (lassen), Schnittstellen mit der x-Achse markieren, fertig. Je nach Fall ergeben sich damit zwei, eine oder gar keine Nullstellen.
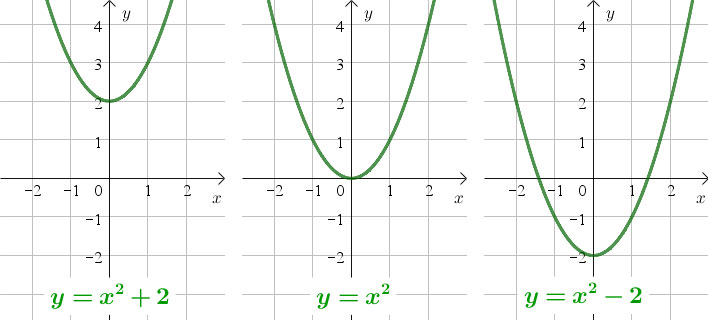
Andererseits wissen wir aber auch, dass jedes Polynom zweiter Ordnung zwei Nullstellen hat (Fundamentalsatz der Algebra). Wenn diese im Graph nicht sichtbar werden, dann sind sie offenbar komplex, besitzen also einen Imaginärteil. Haben Sie sich schon einmal gefragt, wie Sie auch diese komplexen Nullstellen auf einfache Weise visualisieren können? Das geht tatsächlich und ist ziemlich cool. Was Sie dafür benötigen, ist die sogenannte Phantomparabel. Ich beschreibe zunächst die Vorgehensweise und liefere im Anschluss daran den mathematischen Hintergrund.
Die Vorgehensweise
Wir betrachten beispielhaft die Parabel mit der Gleichung y = x^2+2 . Sie hat keine reellen Nullstellen. Um die komplexen Nullstellen sehen zu können, müssen Sie zunächst einmal die komplexe Zahlenebene sichtbar machen. Es ist die Ebene, in der natürlich auch die x-Achse enthalten ist. Sie liegt gewissermaßen “unter” der Parabel:
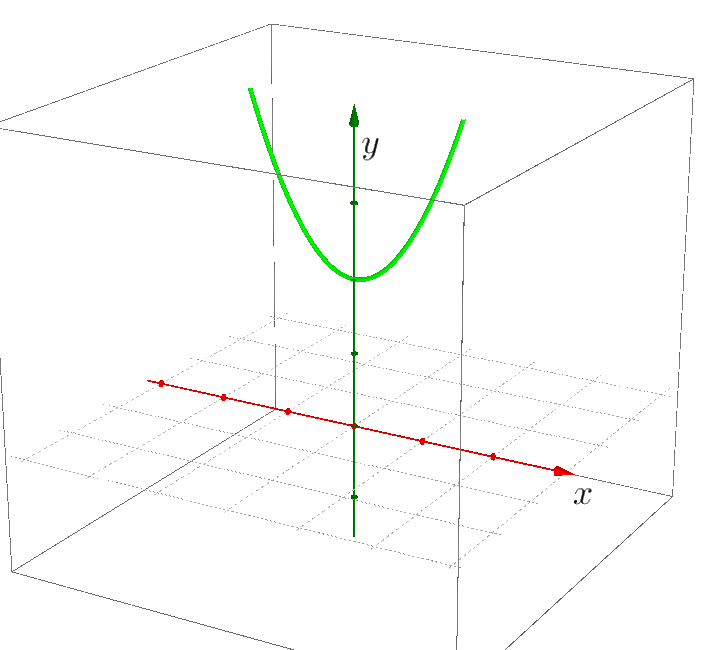
Nun klappen Sie die Parabel am Scheitelpunkt nach unten:

Die so erhaltene orange Parabel drehen Sie um 90° (um die Achse durch den Scheitelpunkt).

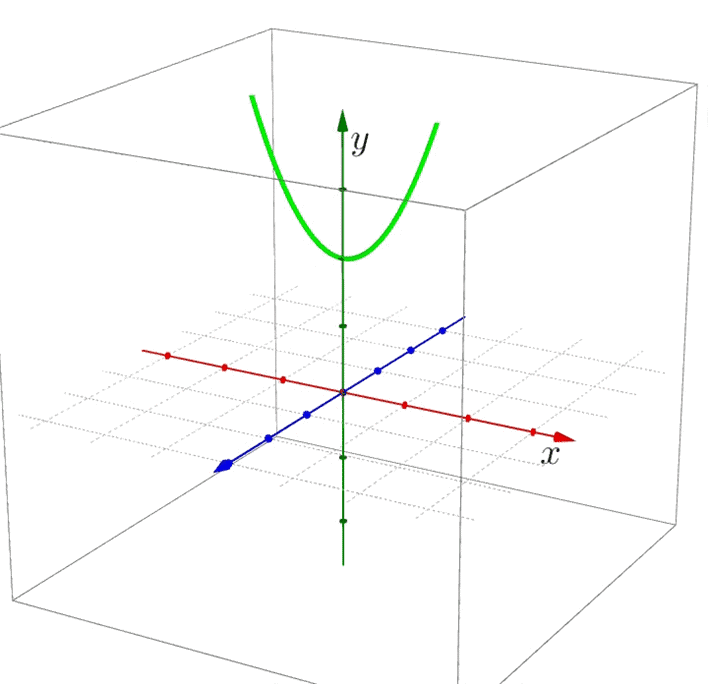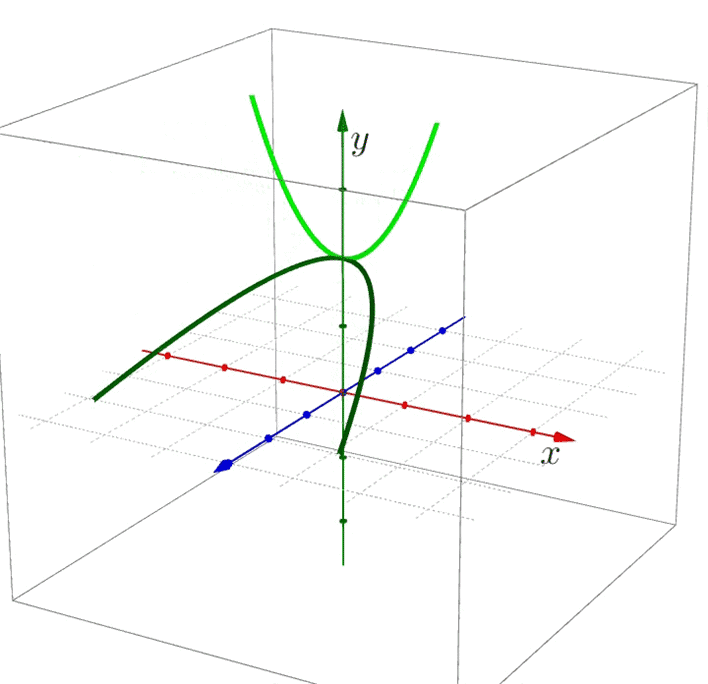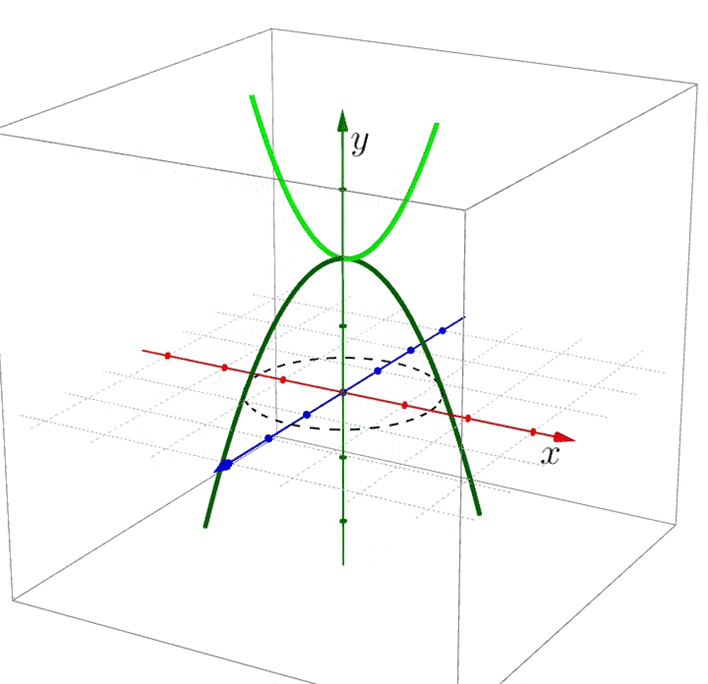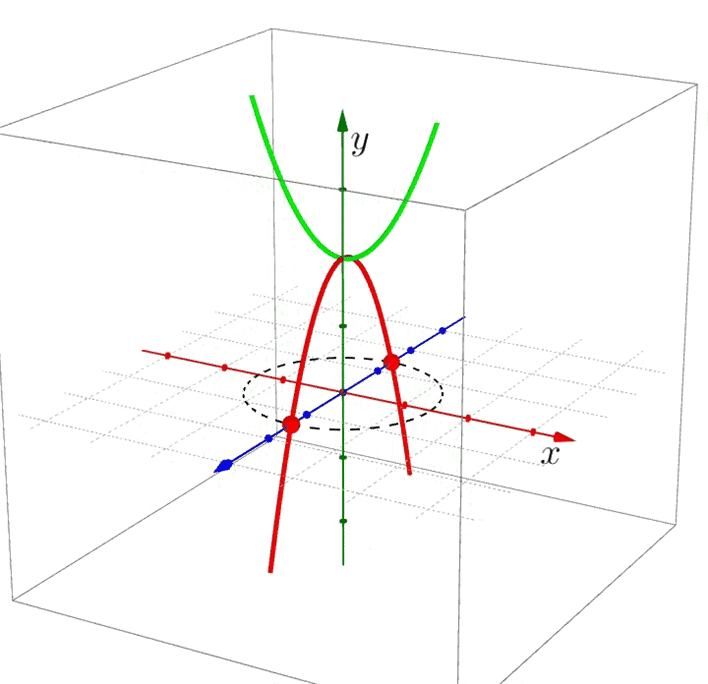
Et voilà: Fertig ist die Phantomparabel. Ihre Schnittpunkte mit der Zahlenebene entsprechen den komplexen Nullstellen der ursprünglichen Funktion: \pm i\sqrt{2} . Das sind genau die beiden Abschnitte auf der imaginären (blauen) Achse.

Hier können Sie die Parabel zusammen mit ihrem Phantom noch einmal in einer animierten Darstellung bewundern:

Und hier ist die ganze Konstruktion auch noch einmal als Animation zu sehen:
Zusammenfassen lässt sie sich also mit den Worten:
Die mathematischen Hintergründe
Wie lautet nun die mathematische Begründung für diese Konstruktion? Um diese Frage zu beantworten, wollen wir davon ausgehen, dass die quadratische Funktion, deren Nullstellen wir visualisieren wollen, in der Form y = ax^2 +c vorliegt. Wenn dies nicht der Fall sein sollte, können wir durch einfache Transformationen diese Form herstellen (siehe unten). Da x ausdrücklich komplex sein darf, schreiben wir es in der Form x = m + ni und fragen, welche Werte x annimmt, wenn y = 0 ist.
y ist nach Voraussetzung reell – wir betrachten ja nur die Funktionswerte über der reellen Achse. Also muss x entweder rein reell oder rein imaginär sein. Das verstehen wir, wenn wir x^2=(m+ni)^2=m^{2} - n^{2} + 2 \; i \; m \; n betrachten. Der imaginäre Teil entfällt, wenn m = 0 (d. h. x ist rein imaginär) bzw. n=0 (d. h. x ist rein reell).
Falls x rein reell ist, gilt also n=0 und damit auch y = ax^2 + c = am^2 + c . Dies ist die Gleichung der Originalparabel über der reellen Achse.
Falls x rein imaginär ist, gilt m = 0 und daher y = a(ni)^2 +c . Dies lässt sich vereinfachen zu y = -an^2 + c . Das ist die Gleichung der Phantom-Parabel über der imaginären Achse!
Das negative Vorzeichen vor dem a ist ein Hinweis darauf, dass die Phantom-Parabel nach unten geöffnet ist. Außerdem ist sie gegenüber der Originalparabel um 90° gedreht, denn sie erstreckt sich über die imaginäre n -Achse, während die Originalparabel nur über der reellen m -Achse verläuft.
Die Nullstellen der beiden Parabeln ergeben sich durch einfaches Umformen zu m = \pm\sqrt{\frac{-c}{a}} bzw. n = \pm\sqrt{\frac{-c}{-a}} . In unserem Beispiel ist a = 1 und c = 2 . Auf der (reellen) m -Achse erhalten wir keine Lösungen, dafür aber auf der (imaginären) n -Achse: n_{1,2} = \pm\sqrt{\frac{-2}{-1}} = \pm\sqrt{2} .
Diese Argumentation funktioniert für jede Parabel. Sollte sie in der Form y = ax^2 + bx + c vorliegen, können Sie sie auf Scheitelpunktform y = a(x-d)^2+e bringen, und (x-d) durch die Substitution v = x-d ersetzen.
Jede Parabel besitzt also eine Phantom-Parabel, und wenn Sie beide zeichnen, können Sie auf diese Weise alle Nullstellen der zugehörigen quadratischen Funktion visualisieren. Wenn diese reell sind, durchstößt die Originalparabel die komplexe Zahlenebene an den entsprechenden Stellen der x -Achse, und die Phantom-Parabel “hängt” unterhalb der Ebene. Und wenn es eine doppelte Nullstelle ist, dann berühren sich Original- und Phantomparabel in genau einem Punkt auf der x -Achse. All diese Fälle können Sie selbst einmal durchspielen – dazu finden Sie hier ein entsprechendes Geogebra-Applet.
Die Idee zur Phantom-Parabel hatte der neuseeländische Mathematiklehrer Philip Lloyd. Sie reicht übrigens noch viel weiter – denn Phantomkurven findet man nicht nur für Parabeln sondern auch für viele andere Funktionsgraphen, die Lloyd in seinem Blog phantomgraphs.weebly.com vorstellt und diskutiert (englischsprachig). Die Vorgehensweise ist dann z. T. erheblich komplizierter.
Die Phantom-Parabel allerdings ist so übersichtlich, dass sie ein hübsches Thema für schulische Mathe-Clubs oder mathematische Arbeitsgemeinschaften sein kann, z. B. wenn diese sich mit dem Thema “imaginäre Zahlen” beschäftigen wollen. Ich habe mit diesem Thema in solchen Zusammenhängen schon für viel Staunen bei Schülerinnen und Schülern gesorgt.