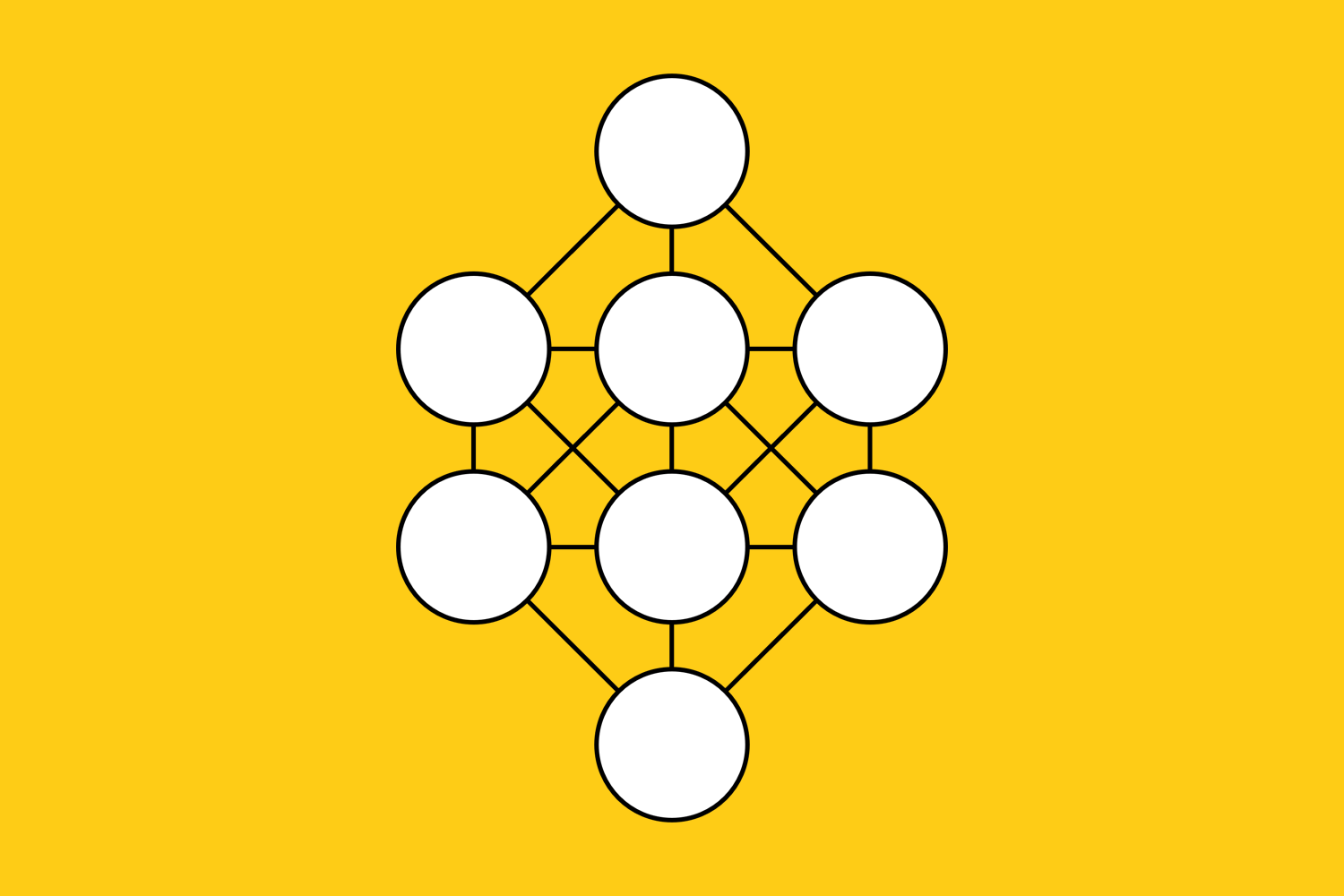
Die Zahlen von 1 bis 8 sollen in den hier abgebildeten 8 Kreisen eingetragen werden. Dabei sollen aber benachbarte Zahlen nicht in Kreise gesetzt werden, die direkt durch eine Linie miteinander verbunden sind. Wenn z. B. die 4 im obersten Kreis steht, dürfen weder 3 noch 5 in einem der drei Kreise in der Zeile darunter eingetragen werden, weil jeder dieser Kreise mit einer direkten Linie mit dem obersten Kreis verbunden ist. Abgesehen von Drehung oder Spiegelung gibt es nur eine einzige Lösung. Finden Sie sie?

Um die Lösung zu erhalten, schreiben Sie mir: loesung@mathematik-unterrichten.de